Una función cuadrática es una función polinómica de grado 2. Tiene una expresión del tipo (forma estándar):

La gráfica de una función cuadrática es una parábola.

Algunas parábolas cortan al eje de las X (eje de abcisas) en dos puntos. Esos valores son las raíces (reales) o ceros del polinomio.

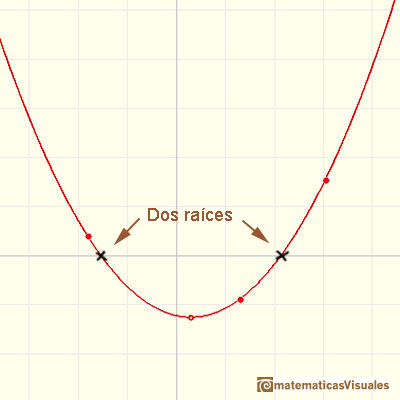
Podemos obtener esas raíces resolviendo una ecuación cuadrática:

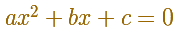
Las soluciones de una ecuación cuadrática vienen dadas por:

El discriminante se define como:

Si el discriminante es mayor que 0, la ecuación cuadrática tiene dos raíces reales, x₁, x₂. En este caso, podemos escribir la función cuadrática descompuesta en sus factores de esta manera:

Algunas parábolas solo tocan al eje de abcisas en un solo punto.

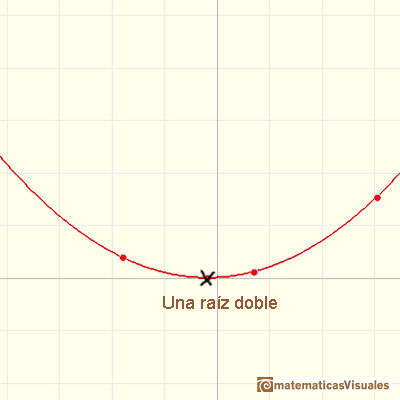
Esto ocurre cuando el discriminante es igual a cero y la solución de la ecuación cuadrática es:

En este caso decimos que la raíz es una raíz doble. La función cuadrática se factoriza así:

Algunas parábolas no tocan ni cortan al eje de las x. En este caso, el discriminante es menor que cero y la ecuación cuadrática no tiene soluciones reales.

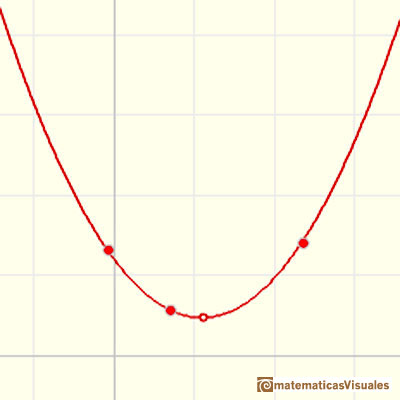
Cuando el coeficiente a es un número positivo, la parábola se abre hacia arriba y si a es un número negativo se abre hacia abajo. Aquí podemos ver más ejemplos de parábolas con dos raíces reales, con una sola raíz doble y sin raíces reales:

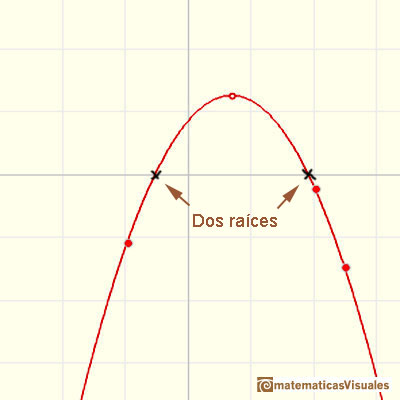
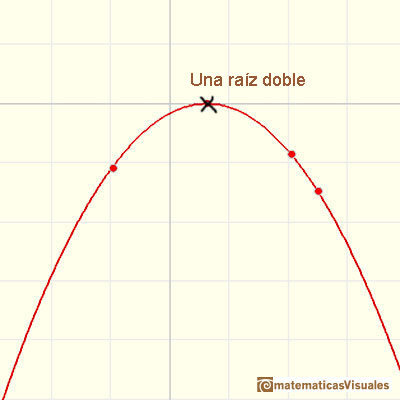
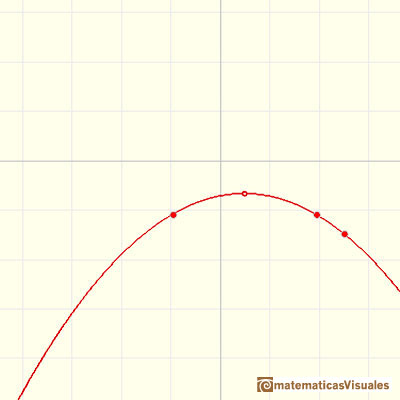
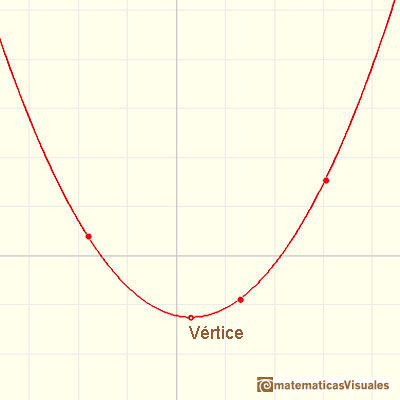
Cada parábola tiene un máximo o un mínimo (tendrá un máximo si el coeficiente a es un número negativo y tendrá un mínimo si ese coeficiente es positivo). Este punto se llama vértice de la parábola. La recta vertical que pasa por el vértice es el eje de simetría de la parábola. La ecuación del eje de simetría es:

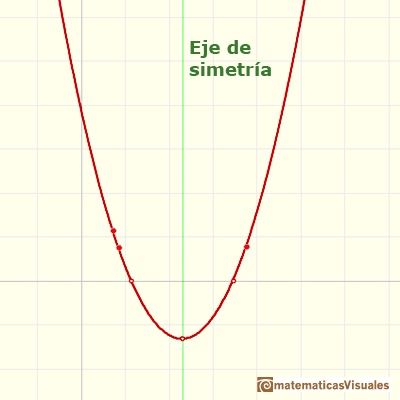
El vértice de la parábola tiene coordenadas: